Mediffuse: CT ↔️ MRI Diffusion-Driven Cross-Modal Translation
Imagine converting a CT scan into a photorealistic MRI—and back again—in under 6 seconds, without specialized hardware or months of tuning. That’s the power of Mediffuse, our CS6384 Computer Vision course project at UTD, harnessing cutting-edge diffusion techniques to bridge imaging modalities like never before.
Tech Stack 💻 & Resources📚
Computer Vision Diffusion Models InstructPix2Pix PyTorch Hugging Face
Authors: Saurav Dosi, Pratiksha Aigal, Animesh Maheshwari, and Varad Abhyankar
Course: CS 6384 - Computer Vision, taught by Dr. Yapeng Tian, The University of Texas at Dallas
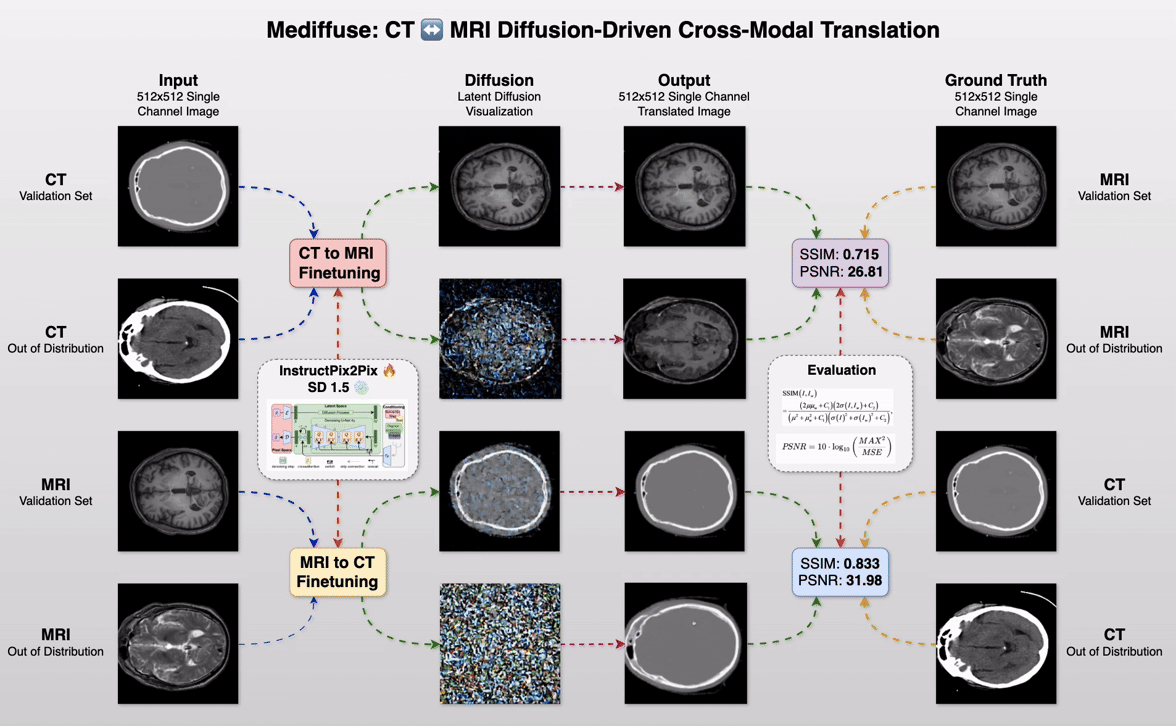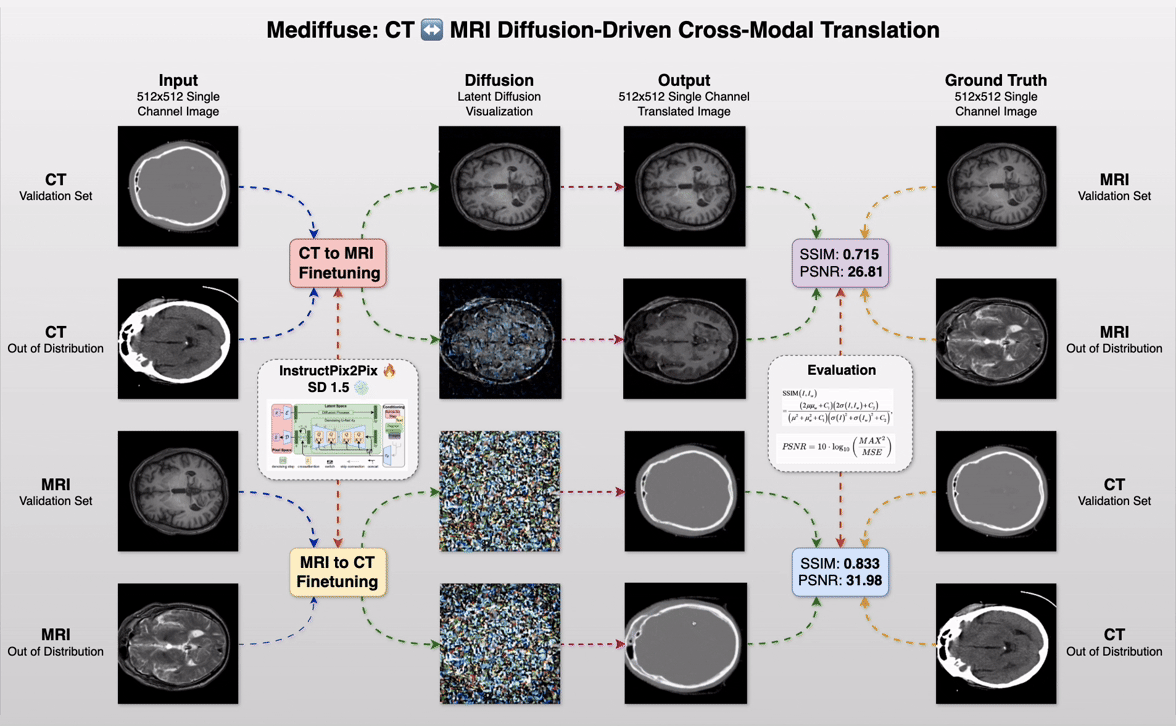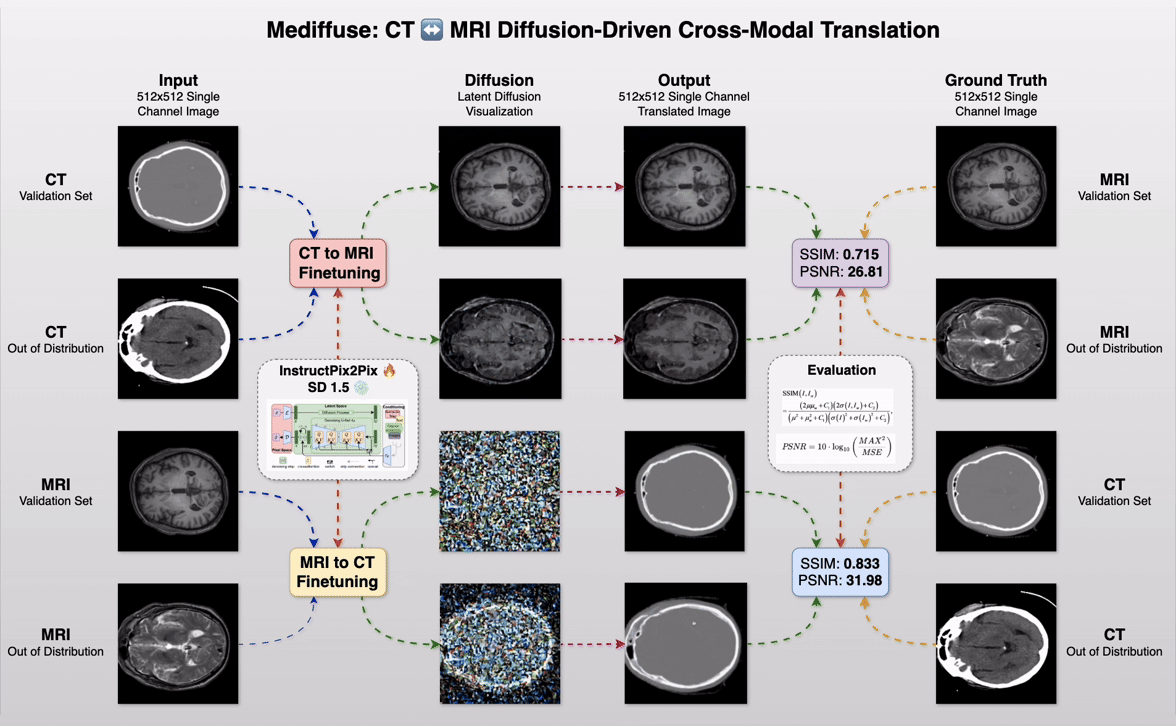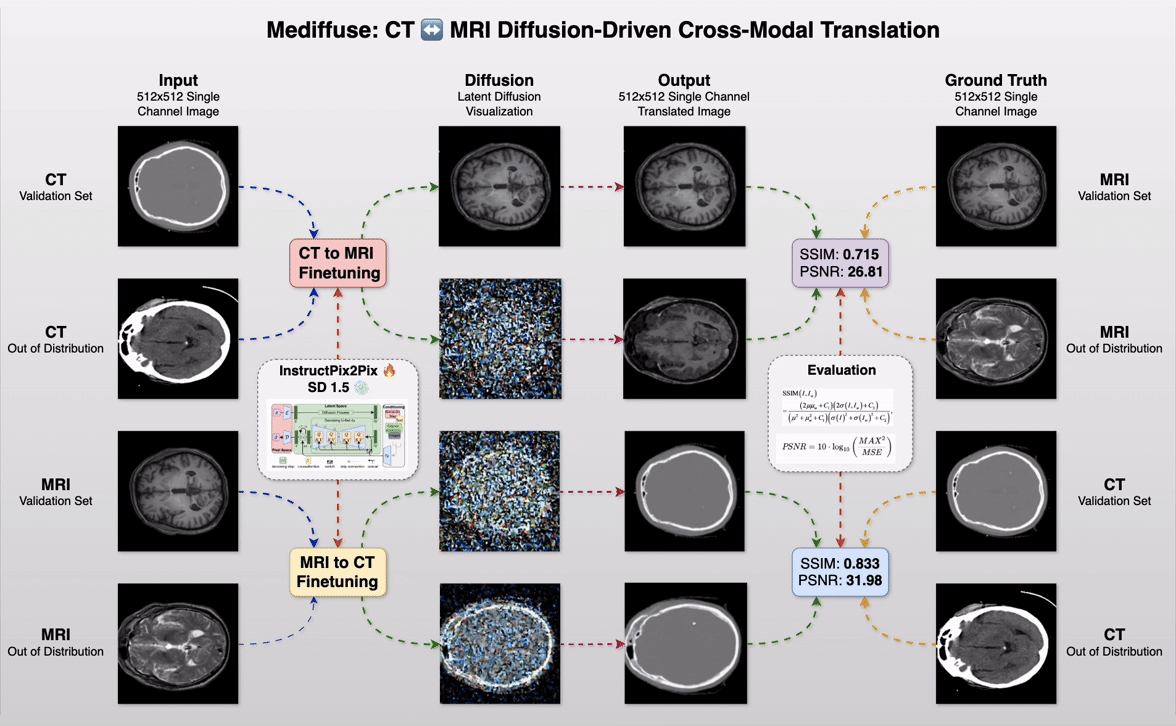
Project Workflow GIF.